Application Examples

In the final section we shall discuss a number of special cases which are important for the experimental application.
 

1) One layer

There are two possible situations: the layer has either a smaller or a larger d than the substrate. What kind of signal do we expect in each case? It δ of the film is smaller than δ of the substrate (e.g. silicon film on a gold surface), we will first reach the critical angle of the film starting from zero incidence. Beyond the critical angle the wave will penetrate the film and reach the substrate which still totally reflects the incident wave. Hence there will be strong interference fringes between the critical angle of the film and the critical angles of the substrate, the so-salled Kiessig fringes (H. Kiessig, Ann. Phys. Leipzig 10, 769 (1931).). In the other situation (Au on silicon), the reflectivity from the film-substrate interface is already quite low by the time the wave penetrates through the the film and we will see only weak fringes in the tail of the reflectivity curve.
 
 

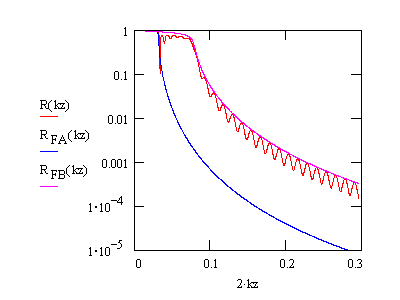
Low Z film on high Z substrate. The reflectivity curve (red) features strong oscillations between the critical angles of the two materials. The minima are related to excitation of a waveguide mode in the film (see below). Above the substrate critical angle regularly spaced oscillations, also called Kiessig fringes, appear. The blue curve (film) and the magenta curve (substrate) show the respective Fresnel reflectivity.

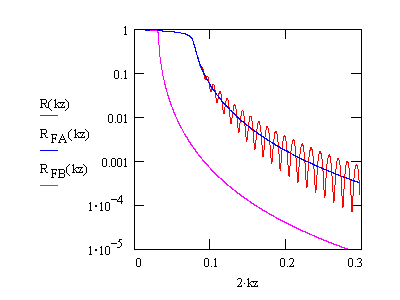
High-Z film on low-Z substrate. The reflectivity curve (red) shows no oscillations between the critical angles; moreover, the Kiessig oscillations only start gradually beyond the critical angle of the film. The blue (film) and magenta (substrate) curves show the Fresnel reflectivity.

The smallest layer spacing observable is given by the signal-to-noise of the experimental set-up. Typically 6 (rotating anode) to 8 orders (synchrotron radiation) of magnitude of the reflected intensity are detected. In the latter case the limit of detection is around 10Å layer thickness. This is enough to see a single monolayer of molecules, for instance fatty acids or lipids at the air-water interface or thiols (Self-Assembled Monolayers) on gold surfaces with a typical thickness between 15 and 30Å.
 

2) Two Layers: Waveguide Modes

If we make a special structure, for example Si:C:Si (bulk), the wave can be trapped by total external reflection between the Si substrate and the Si top layer and travel parallel to the surface in the C layer: We have made a wave guide for x-rays.

The wave guide will trap modes, if the thickness of the C layer matches n π/k'_z , n=1,2,3,... - then we have the nodes of the trapped wave on the top- and bottom interface of the wave guide. The excitation of such a waveguide mode will show up as a sharp dip in the reflected intensity - the dip will be the sharper and shallower, the less damping or losses the guided mode experiences. The wave guide layer in the example below is 500Å thick and covered with a 50Å top layer of the substrate material. Five resonances can be observed between the critical angles.

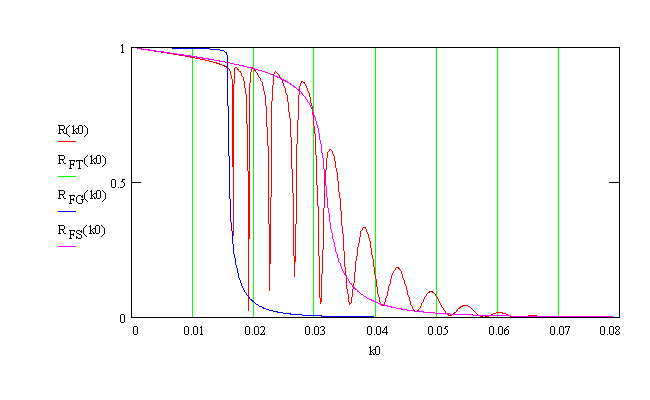
The blue and magenta lines indicate the Fresnel reflectivities of the guiding layer and the cladding layer, respectively.
Beyond the critical angle of the substrate, thickness oscillations appear that can be used to characterize the waveguide structure.
 
 

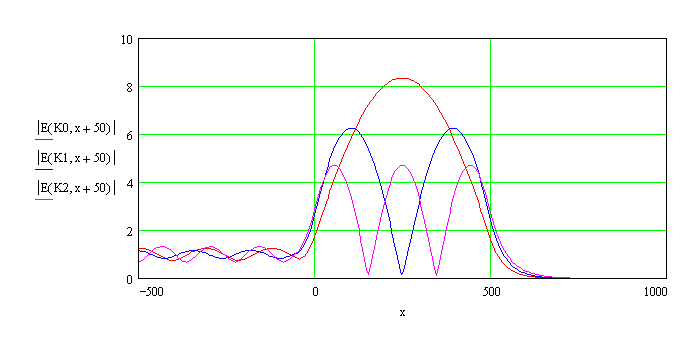
Wave amplitudes associated with the first three resonances TE0, TE1, TE2. For the 0th order resonance (no node) the field is amplified by a factor of 8, i.e. the energy density is 60 times higher than in the incident beam !
 

In the guided mode the electrical field is enhanced. Mike Bedzyk and co-workers at CHESS have shown, how the enhanced field can be used to detect fluorescence from dopant atoms in the layer. In fact, if the concentration and spatial distribution of the dopant atoms is known well, it can be used to measure the electric field in turn. Not only the fluorescent yield but also diffuse scattering experiences such a resonant enhancement. This effect can be used to study defects, nano particles, or lateral density variations in the guiding layer.

Eventually the guided wave will travel to the edge of the substrate or an uncoated part of the substrate and radiate into air. This guided wave is coherent and very compressed in height. Wave guides have been used as microfocussing optical elements.

Actually even a single layer of lower electron density than the substrate will give rise to wave guide modes between the critical angles, as can be seen in the above example for the one-layer case. Naturally the resonances are leakier in the one-layer mode, hence the resonances broaden close to the substrate critical angle. Nontheless, Jin Wang and coworkers have shown that the resonances can be used for resonance-enhanced GISAXS, for which the TE0 mode is particularly useful. Jin Wang and coworkers also showed that the higher-order modes can be used for slicing the layer into different active parts according to to the electric field strength, and thus gaining more detatiled information about the distribution of materials inside the film.

3) Multilayers

If a periodic structure of layers with different refractive indices is prepared, we will get "Bragg reflection" at the corresponding angle. The width of this Bragg peak depends on how many layers contribute to the scattering, i.e. the penetration depth. The angular width of the Bragg peak is directly related to the energy-acceptance at fixed angle by Bragg's law. Thus a W:C multilayer accepts a bandwidth of 2-3% at 10 keV, whereas a Mo:B₄C layers has a bandwidth around 1-1.5%. Another advantage of a Mo-based multilayer is that there are no absorption edges within the G-line energy range from 8 to 16 keV.
 

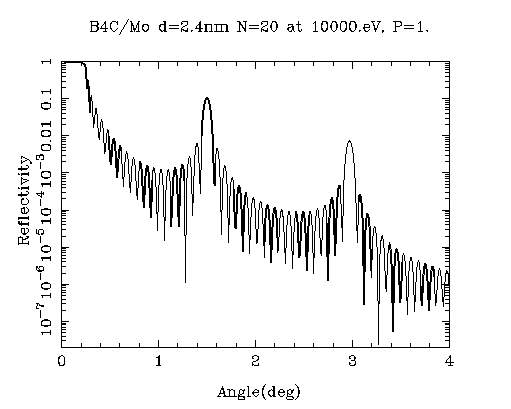
Multilayer reflectivity as calculated with the help of the CXRO web site. In this example the top layer is B₄C, the bottom layer is Mo, with a thickness of 1/3 of the multilayer period of 24Å. A total of 20 layers are used and ideal interfaces are assumed. The G-line multilayers will actually use 200 periods, so the diffraction peaks will be about 10 times sharper (the actual factor is determined by the x-ray attenuation). In this case a reflectivity close to 100% can be achieved for the first order multilayer peak. With a realistic interlayer roughness of 3-4Å we expect reflectivities of better than 50% based on some first test pieces.
 
 

4) Free-standing layers

We can also use our formulism to study free-standing layers. Classic examples are soap films or liquid crystal films that can be suspended in a frame and are pulled flat by the surface tension. Such films can be as thin as 100Å, i.e. cannot be analyzed with optical techniques. From such systems we can look at either the reflected or the transmitted intensity. For practical purposes the reflectivity yields the better information - it is much easier to measure a small signal on a small background than measure the small deviation in the high transmission of the incident x-ray beam.
 
 

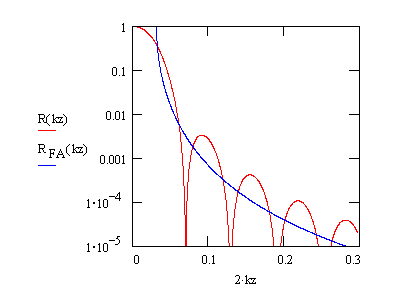
Reflectivity (red) of a freestanding 100Å film. For comparison the Fresnel reflectivity of the bulk  material is shown in blue.

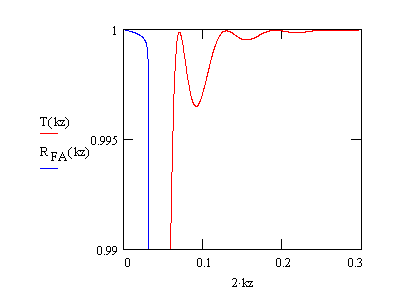
Transmissivity of the same 100Å film. The variations within the transmittivity amount to only fraction of 1%. The blue curve shows the Fresnel reflectivity and the critical angle of the bulk material.