Wave Vector Boundary Conditions at the Interface between two Media

Detlef Smilgies

Let us consider a wave travelling through medium 1 and hitting a plane interface with medium 2. The most general situation will be that part of the incident wave is reflected and part of it refracted into medium 2. The solutions of the wave equation in both media are subject to boundary conditions at the interface. First of all, the frequencies of the three waves must be equal on either side of the interface:

ω = ω'

The dispersion relation for plane waves w² = c² k² implies for the wave vectors:

k'² = n² k²

The next condition is that the wave vector components parallel to the interface are equal - only this way we can have continuity of the fields across the interface:

k'_|| = k_||

From these two boundary conditions we can calculate the relation between the z-components of the wave vector:

k'_z² = k'² - k'_||² = n² k² - k_||² = n² k² - (k² - k_z²) = (n²-1) k² + k_z²

In the introductory chapter we had already seen that the real part of the refractive index for x-rays is slightly less than 1

n = 1 - δ+ i β

with d on the order of 10^-5. The imaginary part b takes account of the absorption.

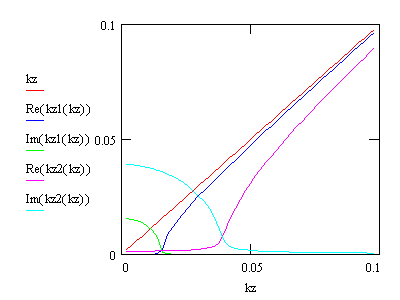
The Figure shows the z-component of the k vector: kz in vacuum, kz1 for a low-Z material (Si), kz2 for a high-Z material (Au), all at a photon energy of 10 keV corresponding to k = 5 A^-1.

If the right hand side turns negative of the equation for k'_z, the wave cannot propagate inside the medium any more, and we have external total reflection. Ignoring b, we get for the critical wave vector using k = ||k|| :

Re(k_z,c) = ( (1-n²) k²)^0.5 = ( 2δ-(δ²-β²) )^0.5 k

For the critical angle a_c we re-derive the well-known result from Snell's formula:

α_c = k_z,c / k = (2δ)^0.5

Suggested reading, e.g. in an electrodynamics text book:

review of the reflection law: k_|| || k_r||
review of Snell's law for the refracted wave

Snell's Law

In x-ray scattering a different angle convention is used compared to visible optics: while in visible optics angles are referenced with respect to the surface normal, in x-ray scattering angles are given relative to a reference plane, which can be the surface plane or a Bragg plane. In the first case the optical and the x-ray angular values simply add up to p/2.

Hence Snell's law for the angle definition in x-ray scattering is written:

cos(α) = n cos(α')

At total external reflection, a' becomes 0, and we get for the critical angle

cos(α_c) = n

Both numbers are close to 1, and expansion yields

1 - α_c² / 2= 1 -δ

with the well-known result from above.

Wave vector as a function of scattering angles

Our basic expression

k'_z² = (n²-1) k² + k_z²

can be further rewritten in terms of the scattering angles:

k'_z² = k² (n²-1 + k_z²/k²) = k² {n²-1 + sin²(α)} = k² {n²-1 + sin²(α)} = k² {n²- cos²(α)} = k² {cos²(α_c)- cos²(α)} = k² {sin²(α) - sin²(α_c)} using cos²(x)=1-sin²(x) for the final step

This way the wave vector inside the film can be related to the wave vector outside the film. Note if a becomes smaller than a_c the wavevector of the scattered wave becomes imaginary - only an evanescent wave travelling parallel to the surface can be inside the film. The scattering inside the film is thus described by the wave vectors of trhe incident and scattered waves inside the film. This refractive correction is important for small qz values.